Рассылка закрыта
При закрытии подписчики были переданы в рассылку "Занимательные задачи и головоломки" на которую и рекомендуем вам подписаться.
Вы можете найти рассылки сходной тематики в Каталоге рассылок.
Логика для всех
"Логика для всех" выпуск No8 oт 2001-04-08
|
Здравствуйте! Сегодня в выпуске:
Практически все присланые ответы оказались правильными. Но решения приводили только представители мужского пола. Честь им и хвала! :) Они постарались не запутаться в пяти похожих женских именах, и при этом все-таки выяснили, кто во что был одет.
Dress Parade
Помните, как у Есенина:
Прислали правильные ответы и решения (кажется, никого не забыла):
(перечисление в порядке поступления писем)
А вот, собственно, и сами решения:
Арсен Кириллов:
Сергей Свириденко:
Олег Домокеев:
Василий Славутинский:
Олег Танасевич:
Ответ: Белла.
Леонид Ляпустин:
Владимир:
Среди писем с ответами и вопросами обнаружила и такое письмо. Привожу его почти полностью. Надеюсь, что кого-нибудь оно заинтересует.
Subject: Да здравствует Логика!
Свершилось! Наконец-то! Я готов прыгать от потолка до радости ... или наоборот?.. Вот! Клянусь квантором, я так давно грезил ночами об этой рассылке, сам того не зная, и только теперь понял, что именно эту рассылку я знал и любил всю свою жизнь! Создатели модальных логик не придумали еще такую модальность "НесказАнно рад, что...", которую обозначим ++. Тогда, если через A обозначить высказывание "Вадим получает рассылку <Логика для всех>", то истинное положение дел описывается формулой ++A. Надеюсь, кому-нибудь еще (кроме меня самого) будут полезны результаты моих поисков в электронных и просто библиотеках. Всем логикам настоятельно советую заглянуть на http://www.philosophy.ru (и дальше вглубь по ссылкам) -- институт философии РАН. Среди прочего там имеется электронная библиотека, в которой и основополагающие трактаты Аристотеля, и классические работы Фреге, Рассела, Витгенштейна, и многое другое. Там я нашел архиинтереснейшую книгу Г.Гутнера "Онтология математического дискурса" -- незаменима для тех, кто ломает себе голову над проклятыми вечными вопросами философских оснований математики и логики. Какой онтологический статус имеют логические законы? В каком смысле "существуют" математические объекты? Впрочем, абсолютизировать и превозносить работу Гутнера не стану. Она интересна, даже очень, но это не делает ее истиной в последней инстанции. Из бумажных книг настоящим интеллектуальным откровением для меня стала "Логика науки" А.А.Зиновьева (да-да, того самого, который "Зияющие высоты"), написанная -- страшно подумать -- в далеком 1971 г! Насколько Зиновьев опередил тогда свое время, видно уже потому, что в работах 2000 года, принадлежащих перу вроде бы серьезных ученых, солидных и титулованных, налицо искреннее ненаигранное непонимание вещей, которые для Зиновьева были тривиальными уже тогда! Меня просто распирает от желания говорить, говорить, говорить об этой книге, но пусть лучше она сама за себя скажет. Но... должен предупредить. Книга требует очень серьезной подготовленности. Недозревший читатель может пожать плечами и презрительно фыркнуть: "Ну и что же здесь такого? Переливание из пустого в порожнее!". Это как айсберг: 90% под водой. Буду более чем благодарен любому, кто покажет линк, где эта книга (и/или, быть может, другие логические работы Зиновьева и/или сходные по духу) лежат в электронном виде. Быть может, кто-то знает, как с Самим Зиновьевым (да продлятся дни его!) связаться по емейлу? (Есть несколько вполне конкретных вопросов, которые хотелось бы задать автору.) А теперь, братья-логики, прошу помочь! Кто знает, где добыть в электронном виде работы Готлоба Фреге (создатель первого в мире исчисления предикатов, основоположник интенсиональной логики), можно в оригинале -- по-немецки, можно в английском переводе, но если по-русски -- тоже так и быть сойдет? (Кроме трех статей "О смысле и значении", "Отрицание..." и "Мысль...", которые я уже нашел в эл. библиотеке ИФРАН.) Где вообще откопать электронные труды по интенсиональным и релевантным логикам? Где добыть (в электронном виде) знаменитейшую эпохальную Principia Mathematica? И, наконец, главное. Вот проблема. Дана некоторая область реальных (жизненных, практических) задач. Ясно, что для разных классов задач характерны свои приемы рассуждения, а значит -- своя прикладная логика. То есть первоначально единая логика в многообразии приложений расщепляется в семейство (спектр) частных (прикладных) логик. А над всеми этими частными логиками стоит единая металогика -- общие законы построения прикладных логик. Для отдельно взятых классов задач прикладных стоит проблема построения соответствующих прикладных логик. Для последних, в свою очередь, стоит проблема обоснования адекватности задачам (почему именно эта, а не другая логика выбрана в качестве прикладной логики данного класса задач). А на метауровне стоит метапроблема: построение метазаконов построения прикладных логик, увязывание прикладных логик в систему, установление связей, отношений ("интерфейсов") между ними. Собственно, именно об этом идет речь в "Логике науки" А.А.Зиновьева. Киевская школа теории программирования (акад. В.Н.Редько) решает эту (мета)проблему в несколько более конкретизированном варианте -- в приложении к программированию (построение общей металогики всего программирования + развертывание семейства частных логик для прикладных программирований). Это называется "экспликативное программирование". Так вот. ИЩУ КОЛЛЕГ! Все, кто прямо или косвенно занимается проблемами прагматико-ориентированной экспликации логики, прошу, откликнитесь! Где Вы? АУ! vvin@ratibor.zt.ukrtel.net, vvinnik@ziet.zhitomir.ua -- Вадим Юрьевич Винник <...> Да хранит тебя модус поненс! Вадим
А теперь отвечу на некоторые вопросы, встречающиеся в письмах. Многие спрашивают, почему на сайте "Логика для всех" пока мало что работает и часто встречается "under construction". Со временем все (или почти все) появится - что-то в работе, что-то оформляется... Занимаюсь наполнением по мере сил, времени и настроения. О том, что из учебных материалов будет в рассылкe, можно прочитать здесь. А о том, что уже было - в архиве рассылки на сайте и на Subscribe.Ru. Не стесняйтесь спрашивать, если что-то неясно. Открою маленький секрет: у меня нет русской клавиатуры, и мне постоянно приходится использовать конверторы и транслитераторы, а это страшно тормозит работу (и является причиной досадных опечаток и ошибок, к коим я весьма трепетно отношусь), поэтому не удивляйтесь, если я отвечу вам латиницей - просто, так быстрее... Если вы присылаете свое решение в первый раз, указывайте, пожалуйста, свое имя (так как вам хотелось бы называться на страницах рассылки), город, страну... У меня нет пока четкой позиции относительно публикации адреса электронной почты (спам не спит), поэтому лучше называть url'ы (если есть). Присылайте свои пожелания по оформлению рассылки, частоте выхода, объему, темам и др. Постараюсь все принять к сведению. А напоследок, хочется отдельно поприветствовать казанских (надеюсь, таковые есть) подписчиков (нет слов, чтобы передать тоску по родному городу и друзьям) и израильских (а таковые, судя по статистике, есть) :-). Ниже приведены некоторые из задач предыдущих выпусков рассылки (для присоединившихся недавно). Решайте в свое удовольствие, а если будет желание, присылайте свои мысли по поводу (и без)... С огромным интересом и вниманием выслушаю (прочитаю) все предложения, замечания, комментарии...
The Old Girls' reunion
Отправить решение: mailto:ntl@yandex.ru?Subject=The Old Girls' reunion
The Three Hotel Visitors
Отправить решение: mailto:ntl@yandex.ru?Subject=The Three Hotel Visitors
Отправить решение: mailto:ntl@yandex.ru?Subject=8 marta
У КОГО КАКОЙ ТУЗ
Отправить решение: mailto:ntl@yandex.ru?Subject=У КОГО КАКОЙ ТУЗ
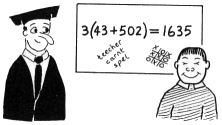
Wong sum 3 (43 + 502) = 1635
Отправить решение: mailto:ntl@yandex.ru?Subject=Wong sum
|
До новой рассылки!
Вопросы, пожелания и замечания пишите на ntl@yandex.ru.
Natalia
http://ntl.narod.ru/logic - Логика для всех
http://book.by.ru/cgi-bin/book.cgi?book=logic - Головоломный форум
Использование материалов рассылки без согласования с ведущим рассылки не одобряется.
Приглашаю к сотрудничеству рекламодателей и спонсоров.
|
| Архив Рассылки | Описание Рассылки | Статистика Рассылки |
|
http://subscribe.ru/
E-mail: ask@subscribe.ru |
| В избранное | ||