| ← Март 2017 → | ||||||
|
1
|
3
|
|||||
|
6
|
7
|
8
|
9
|
10
|
||
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
|
22
|
23
|
24
|
25
|
|||
|
28
|
||||||
За последние 60 дней 1 выпусков (1 раз в 2 месяца)
Сайт рассылки:
http://best.moy-forum.net/
Открыта:
10-08-2009
Статистика
0 за неделю

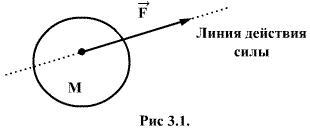
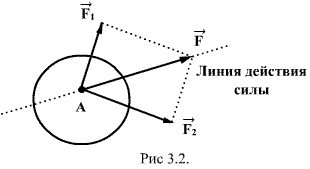
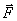 , равно их геометрической сумме
, равно их геометрической сумме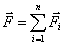 (3.1)
(3.1)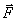 свободное тело изменяет скорость своего поступательного движения, приобретая ускорение
свободное тело изменяет скорость своего поступательного движения, приобретая ускорение 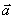 . При этом ускорение тела прямо пропорционально вызывающей его силе и совпадает с ней по направлению:
. При этом ускорение тела прямо пропорционально вызывающей его силе и совпадает с ней по направлению: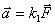
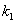 - положительный коэффициент пропорциональности, постоянный для каждого конкретного тела.
- положительный коэффициент пропорциональности, постоянный для каждого конкретного тела.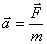 (3.2)
(3.2)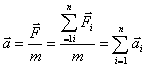 (3.3)
(3.3)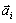 - ускорение материальной точки, вызываемое действием на нее одной силы
- ускорение материальной точки, вызываемое действием на нее одной силы 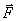 .
.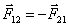
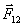 и
и 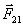 приложены к разным телам и поэтому не уравновешивают друг друга.
приложены к разным телам и поэтому не уравновешивают друг друга.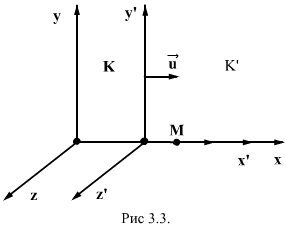
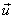 (K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называются преобразованием Галилея
(K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называются преобразованием Галилея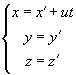
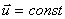 , найдем соотношения между скоростями и ускорениями:
, найдем соотношения между скоростями и ускорениями: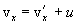
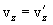
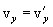
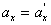
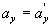
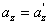
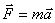
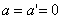 движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея.
движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея.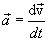 ,
,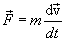 или
или 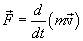
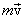 называется импульсом или количеством движения тела и совпадает по направлению с вектором скорости
называется импульсом или количеством движения тела и совпадает по направлению с вектором скорости 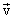 , а
, а 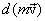 выражает изменение вектора импульса.
выражает изменение вектора импульса.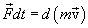 (3.6)
(3.6)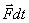 называется импульсом силы
называется импульсом силы 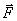 .
.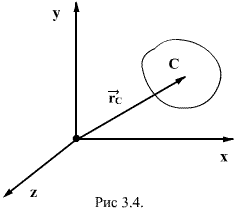
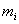 и радиус-векторами
и радиус-векторами 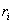 , то центром масс системы материальных точек называют такую т.С, радиус-вектор которой определяется следующим образом:
, то центром масс системы материальных точек называют такую т.С, радиус-вектор которой определяется следующим образом: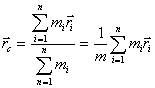 (3.7)
(3.7)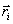 - масса и радиус-вектор i-ой точки системы, m - общая масса всей системы.
- масса и радиус-вектор i-ой точки системы, m - общая масса всей системы.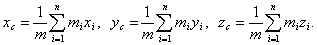
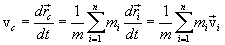 (3.8)
(3.8)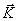 :
: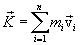 ,
,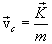 (3.9)
(3.9)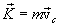 (3.10)
(3.10)



