Еще раз повеселимся.

Еще раз повеселимся.

11 ноября была опубликована на этом сайте забавная задачка для школьников. Вот ее текст:

.======================

Сыну-первокласснику задали на математическом кружке новую задачку. Она, конечно, на логику и соображалку, но все равно очень забавная. Вот такая:
В один прекрасный день один из семи гномов решил, что он будет говорить по вторникам только неправду, а по четвергам и пятницам - только правду. А в остальные дни - как получится, когда правду, а когда неправду.
Соседи 7 дней подряд спрашивали, как его зовут. Первые 6 дней по порядку гном давал такие ответы: Умник, Ворчун, Весельчак, Ворчун, Соня, Ворчун.
Внимание, вопрос: Что ответил гном в последний день?

.=============================

Один из читателей дал совершенно правильный ответ: “Умник». Вот только ответ этот у меня вызвал некоторое чувство недосказанности. Автор совершенно справедливо ограничил круг решений, утверждая,что начало ответов гнома должно приходиться на пятницу, потому что правду гном говорит по четвергам и пятницам, а в списке ответов нет повторяющихся подряд ответов. Все верно. Вот только автор упустил из рассмотрения еще 2 варианта: когда начало ответов приходится на субботу и воскресенье. Итак, налицо3 решения! Анализ показывает, что 2 из них- ложные, так как приводят к противоречию с вторником,когда гном говорит только неправду. Итак, остается только 1 ответ- именно тот, который и предложил читатель. Задача решена. Но почему бы не подойти к ней с научных позиций?

Итак, мы имеем:

Гнома, который то врет, то говорит правду, то вообще неизвестно.

Мы не знаем, с какого дня недели гном начал отвечать на вопросы. Это дает нам 7 вариантов.

Мы не знаем, что сказал гном в последний день опроса(это нам и надо найти). Это дает нам еще 6 вариантов.

Итого, мы должны рассмотреть 6*7=42 варианта.

Будем поочередно подставлять в последний ответ гнома один из шести вариантов и последовательно сдвигать эти ответы по дням недели.

Ну и нам понадобится критерий, по которому мы будем отбирать верные решения (мы заранее не знаем, сколько их будет). В качестве такого критерия примем то, что мы знаем наверняка, а именно:

1. по вторникам гном всегда врет.

2. по четвергам и пятницам он всегда говорит правду, поэтому оба значения должны совпадать.

3. значение вторника не должно совпадать со значениями четверга и пятницы (ложь не может быть равна правде).

    

Без компьютера не обойтись!!

Итак, вот текст программы, написанный на Паскале. Откомпилировать его можно в Delphi (я использую Delphi7). Впрочем, можно использовать любой компилятор Турбо- паскаля, внеся незначительные изменения в заголовок программы.

program Project1;

{$APPTYPE CONSOLE}

uses

SysUtils;

var

//z:array[0..6] of string=('Умник', 'Ворчун', 'Весельчак', 'Ворчун', 'Соня', 'Ворчун','**');

z:array[0..6] of string=('Um', 'Vo', 'Ve', 'Vo', 'So', 'Vo','**');

k,j,i:integer;

begin

writeln;

Writeln(' 0 1 2 3 4 5 6');

Writeln(' * F * T T * *');

Writeln('---------------------------------');

for j:=0 to 5 do

begin

z[6]:=z[j];

writeln;

for i:=0 to 6 do

begin

write(i,' ');

for k:=0 to 6 do write(z[(k+i) mod 7],' ');

if (z[(3+i) mod 7]=z[(4+i) mod 7]) and (z[(1+i) mod 7] <> z[(3+i) mod 7]) then

write('---Result---> ', z[6 ]);

writeln;

end;

end; //for j

readln;

end.

А вот результат ее работы:

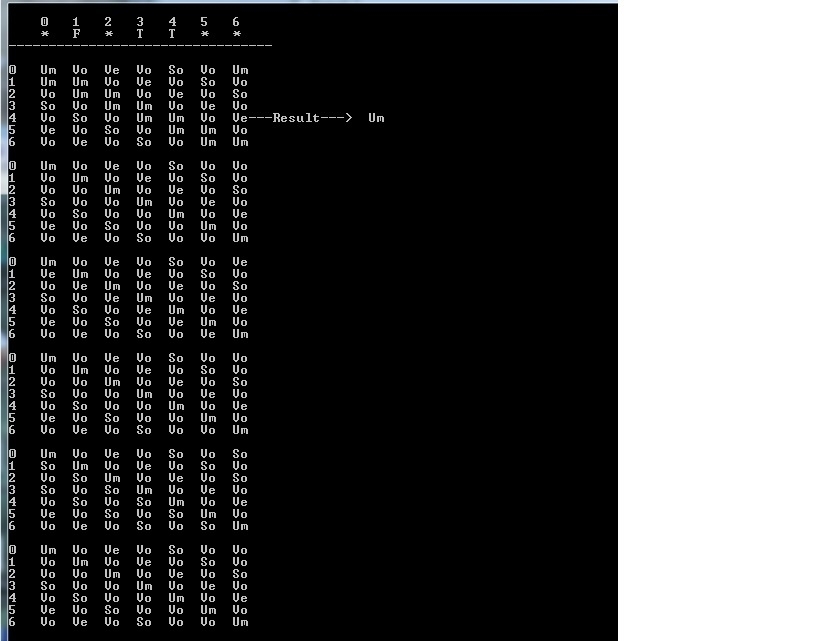
Итак, найдено только одно непротиворечивое решение.

Несколько пояснений:

Я заменил русские имена латинскими 2- буквенными сокращениями (чтобы не возиться с кодировкой).

И еще: вместо того, чтобы сдвигать ответы гнома по дням недели, я провожу циклическую перестановку этих ответов. Но и это я делаю чисто условно- просто изменяя индекс I, который и обозначает начало кольца. Чтобы понять это- напишите все ответы гнома по кругу. Индекс I будет указывать на первый ответ.

И последнее: здесь используется функция mod. Эта функция вычисляет остаток от деления целых чисел. Например, 7 mod 3 даст в ответе 1. Нужна она для того, чтобы индекс I всегда оставался в пределах массива ответов.

Может быть, это пригодится малышам на занятиях по информатике....